Econometria Básica de Gujarati e Porter: Resolvendo Exercícios Propostos
Econometria é uma ferramenta (ou técnica) muito usada por economistas, estatísticos e também por outras ciências. Uma definição encontrada nos livros básicos é:
“Econometria é a aplicação de modelos estatísticos em dados econômicos”
Com base nesta definição, é importante entender a definição de modelos estatísticos e dados econômicos. Em modelos estatísticos, podemos interpretar como equações matemáticas que buscam traduzir um fenômeno estudado, sendo aplicado à coleta, análise e interpretação de dados ou frequência de eventos visando modelar a aleatoriedade e a incerteza. Por outro lado, dados econômicos não possuem uma definição tão clara, porém sabendo que a ciência econômica atua no estudo da alocação dos recursos da sociedade, é possível inferir quando os dados são econômicos.
Estou apresentando estas definições por conta de que neste post irei focar em um livro de Econometria Básica muito usado nos cursos de Economia. O livro foi escrito por Damodar N. Gujarati e Dawn C. Porter e contêm muitos exercícios usando dados econômicos que achei bastante interessante. Pelo fato de o livro não mostrar as soluções dos problemas, achei válido fazer um post com as soluções de alguns dos exercícios.

Os dados usados nos exercícios estarão em meu repositório do Github, em formato “.txt”. Para acessar um dataset, basta usar o seguinte comando:
# Primeiro chame o pacote 'readr' que contém a função 'read_csv'
library(readr)
# Exemplo com o dataset 'table_1.3'
table_1.3_cpi <- readr::read_delim(file = "https://raw.githubusercontent.com/FranciscoPiccolo/franciscopiccolo.github.io/master/datasets/2020-03-01-basic_econometrics_by_gujarati/table_1.3_cpi.txt",
delim = " ")Porém, ao invés de sempre usar este caminho extenso para trazer o dataset, eu posso criar uma variável contendo este caminho e mudar apenas a última parte, em que indico o nome do dataset (i.e. “table_1.3_ipc.txt”).
dataset_path <- "https://raw.githubusercontent.com/FranciscoPiccolo/franciscopiccolo.github.io/master/datasets/2020-03-01-basic_econometrics_by_gujarati/"Com isso, para chamar um dataset, basta usar um comando mais curto, com a função “paste”.
table_1.3_cpi <-
readr::read_delim(file = paste(dataset_path,
"table_1.3_cpi.txt",
sep = ""),
delim = " ")Agora vamos ao que interessa. Para desenvolver os exercícios, vou usar os pacotes abaixo:
library(tidyverse)
library(patchwork)
library(gt)
library(modelsummary)
library(stringr)Capítulo 1
1.1. A Tabela 1.3 apresenta dados relativos ao Índice de Preços ao Consumidor (IPC) de sete países industrializados. A base do índice é 1982–1984 = 100.
a. Com base nos dados fornecidos, calcule a taxa de inflação de cada país.
Vamos trazer o dataset necessário.
table_1.3_cpi <-
readr::read_delim(file = paste(dataset_path,
"table_1.3_cpi.txt",
sep = ""),
delim = " ") %>%
mutate(year = as.character(year))Vamos também ver uma amostra destes dados:
table_1.3_cpi %>%
head(5) %>%
knitr::kable(format.args = list(big.mark = ".", decimal.mark = "."))| year | usa | canada | japan | france | germany | italy | uk |
|---|---|---|---|---|---|---|---|
| 1980 | 824 | 761 | 910 | 722 | 867 | 639 | 785 |
| 1981 | 909 | 856 | 953 | 818 | 922 | 755 | 879 |
| 1982 | 965 | 949 | 981 | 917 | 970 | 878 | 954 |
| 1983 | 996 | 1.004 | 998 | 1.003 | 1.003 | 1.008 | 998 |
| 1984 | 1.039 | 1.047 | 1.021 | 1.080 | 1.027 | 1.114 | 1.048 |
A inflação para cada país será a variação de um período com base no período anterior. Para realizar este cálculo, basta usar o ‘mutate’ e a função ‘lag’.
# Usando o pacote gt (Grammar of Tables) para esse exercício
table_1.3_cpi %>%
mutate(usa_cpi = usa/lag(usa,1)-1,
canada_cpi = canada/lag(canada,1)-1,
japan_cpi = japan/lag(japan,1)-1,
france_cpi = france/lag(france,1)-1,
germany_cpi = germany/lag(germany,1)-1,
italy_cpi = italy/lag(italy,1)-1,
uk_cpi = uk/lag(uk,1)-1) %>%
select(year, usa_cpi, canada_cpi, japan_cpi, france_cpi, germany_cpi, italy_cpi, uk_cpi) %>%
tidyr::gather("country","values", 2:8) %>%
filter(!is.na(values)) -> country_cpi
country_cpi %>%
tidyr::spread("country","values") %>%
gt::gt() %>%
gt::tab_header(title = md("**Inflação (CPI) para os Países Selecionados**"),
subtitle = "De 1981 Até 2005") %>%
gt::tab_source_note(source_note = "Fonte: FMI") %>%
gt::tab_footnote(footnote = "Index = 100",
locations = cells_body(columns = vars(year),
rows = 4)) %>%
fmt_percent(columns = 2:8)| Inflação (CPI) para os Países Selecionados | |||||||
|---|---|---|---|---|---|---|---|
| De 1981 Até 2005 | |||||||
| year | canada_cpi | france_cpi | germany_cpi | italy_cpi | japan_cpi | uk_cpi | usa_cpi |
| 1981 | 12.48% | 13.30% | 6.34% | 18.15% | 4.73% | 11.97% | 10.32% |
| 1982 | 10.86% | 12.10% | 5.21% | 16.29% | 2.94% | 8.53% | 6.16% |
| 1983 | 5.80% | 9.38% | 3.40% | 14.81% | 1.73% | 4.61% | 3.21% |
| 19841 | 4.28% | 7.68% | 2.39% | 10.52% | 2.30% | 5.01% | 4.32% |
| 1985 | 4.11% | 5.83% | 2.04% | 9.25% | 2.06% | 6.01% | 3.56% |
| 1986 | 4.13% | 2.54% | −0.19% | 5.92% | 0.67% | 3.42% | 1.86% |
| 1987 | 4.32% | 3.33% | 0.29% | 4.81% | 0.00% | 4.18% | 3.65% |
| 1988 | 4.05% | 2.64% | 1.33% | 5.03% | 0.67% | 4.93% | 4.14% |
| 1989 | 4.95% | 3.54% | 2.73% | 6.20% | 2.27% | 7.80% | 4.82% |
| 1990 | 4.80% | 3.26% | 2.75% | 6.44% | 3.15% | 9.45% | 5.40% |
| 1991 | 5.61% | 3.24% | 3.65% | 6.30% | 3.23% | 5.87% | 4.21% |
| 1992 | 1.54% | 2.33% | 5.07% | 5.28% | 1.74% | 3.70% | 3.01% |
| 1993 | 1.79% | 2.14% | 4.42% | 4.57% | 1.28% | 1.60% | 2.99% |
| 1994 | 0.20% | 1.67% | 2.74% | 4.05% | 0.68% | 2.42% | 2.56% |
| 1995 | 2.16% | 1.78% | 1.68% | 5.27% | −0.08% | 3.48% | 2.83% |
| 1996 | 1.59% | 2.02% | 1.50% | 3.99% | 0.08% | 2.40% | 2.95% |
| 1997 | 1.63% | 1.19% | 1.85% | 2.06% | 1.84% | 3.18% | 2.29% |
| 1998 | 0.96% | 0.65% | 0.94% | 1.97% | 0.58% | 3.40% | 1.56% |
| 1999 | 1.71% | 0.52% | 0.65% | 1.66% | −0.33% | 1.52% | 2.21% |
| 2000 | 2.74% | 1.68% | 1.43% | 2.52% | −0.66% | 2.99% | 3.36% |
| 2001 | 2.55% | 1.65% | 1.97% | 2.76% | −0.74% | 1.75% | 2.85% |
| 2002 | 2.25% | 1.94% | 1.31% | 2.52% | −0.92% | 1.67% | 1.58% |
| 2003 | 2.78% | 2.08% | 1.09% | 2.66% | −0.25% | 2.90% | 2.28% |
| 2004 | 1.86% | 2.16% | 1.69% | 2.19% | 0.00% | 3.00% | 2.66% |
| 2005 | 2.15% | 1.70% | 1.92% | 1.95% | −0.34% | 2.83% | 3.39% |
| Fonte: FMI | |||||||
|
1
Index = 100
|
|||||||
b. Represente graficamente a taxa de inflação de cada país em relação ao tempo (isto é, use o eixo horizontal para o tempo e o eixo vertical para a taxa de inflação).
country_cpi %>%
ggplot2::ggplot()+
geom_line(mapping = aes(x = year,
y = values,
group = country,
color = country))+
scale_y_continuous(labels = scales::percent)+
scale_x_discrete(breaks = c("1985","1995","2005"))+
scale_color_brewer(type = "qual", palette = 2)+
theme_graph()+
labs(title = "Inflação dos Países Selecionados",
y = "CPI (Consumer Price Index)")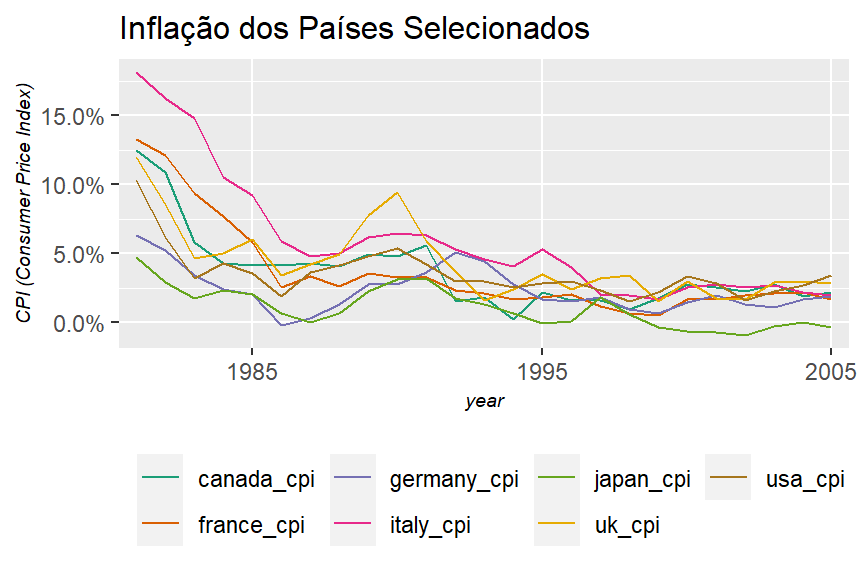
c. Que conclusões gerais é possível tirar sobre a evolução da inflação nos sete países?
Há uma tendência de queda nos países selecionados após 1985, onde todos mantiveram uma taxa abaio de 5% ao ano.
d. Em que país a taxa de inflação parece ser a mais flutuante? Há alguma explicação para isso?
A tabela abaixo mostra um resumo da inflação de cada país, já transformada em percentual.
country_cpi %>%
mutate(values = values*100) %>%
tidyr::spread("country","values") %>%
modelsummary::datasummary_skim()| Unique (#) | Missing (%) | Mean | SD | Min | Median | Max | ||
|---|---|---|---|---|---|---|---|---|
| canada_cpi | 25 | 0 | 3.7 | 2.8 | 0.2 | 2.7 | 12.5 | |
| france_cpi | 25 | 0 | 3.6 | 3.4 | 0.5 | 2.2 | 13.3 | |
| germany_cpi | 25 | 0 | 2.3 | 1.6 | -0.2 | 1.9 | 6.3 | |
| italy_cpi | 25 | 0 | 5.9 | 4.6 | 1.7 | 4.8 | 18.2 | |
| japan_cpi | 24 | 0 | 1.1 | 1.5 | -0.9 | 0.7 | 4.7 | |
| uk_cpi | 25 | 0 | 4.3 | 2.7 | 1.5 | 3.4 | 12.0 | |
| usa_cpi | 25 | 0 | 3.5 | 1.8 | 1.6 | 3.0 | 10.3 |
O desvio padrão (SD) mais elevado é o da Itália, talvez por ter um outlier no valor máximo (de 18.2%). O gráfico abaixo irá dar destaque para este país para vermos se é evidente que sua flutuação é maior que a dos outros.
country_cpi %>%
mutate(is_floating = as.character(case_when(country == "italy_cpi" ~ "Italy CPI",
TRUE ~ "Others"))) %>%
ggplot2::ggplot()+
geom_line(mapping = aes(x = year,
y = values,
group = country,
color = is_floating),
size = 1)+
scale_y_continuous(labels = scales::percent)+
scale_x_discrete(breaks = c("1985","1995","2005"))+
scale_color_manual(values = c("Italy CPI" = "dark orange",
"Others" = "steel blue"),
name = "Inflação da Inglaterra = 1")+
theme_graph()+
labs(title = "Análise da Inflação na Itália",
subtitle = "Aparentemente é a taxa mais flutuante",
y = "CPI (Consumer Price Index)")
A flutuação parece maior na Itália por conta dos primeiros anos, onde a inflação ficou bastante alta. Caso a análise seja feita a partir de 1985, a Inglaterra fica com maior desvio padrão.
1.2
a. Usando a Tabela 1.3, represente as taxas de inflação do Canadá, França, Alemanha, Itália, Japão e Reino Unido em relação à taxa de inflação dos Estados Unidos.
Com o pacote GGally é possível criar estes comparativos mais facilmente.
country_cpi %>%
tidyr::spread("country", "values") %>%
GGally::ggpairs(columns = 2:8)+
theme_graph()+
theme(axis.text = element_blank())+
labs(title = "Correlação Entre as Taxas de Inflação")
Apenas a linha e coluna ‘usa_cpi’ precisa ser usada, mostrando o gráficos de dispersão entre as variáveis e seu coeficiente de correlação. A menor correlação é a da Alemanha, que ficou em 69,3%.
b. Faça um comentário geral sobre o comportamento das taxas de inflação dos seis países em relação à inflação dos Estados Unidos.
country_cpi %>%
tidyr::spread("country", "values") %>%
select(-year) %>%
cor() %>%
knitr::kable(format.args = list(big.mark = ".", decimal.mark = ","))| canada_cpi | france_cpi | germany_cpi | italy_cpi | japan_cpi | uk_cpi | usa_cpi | |
|---|---|---|---|---|---|---|---|
| canada_cpi | 1,0000000 | 0,9031983 | 0,5858029 | 0,8816498 | 0,7205414 | 0,8544959 | 0,8730004 |
| france_cpi | 0,9031983 | 1,0000000 | 0,6567352 | 0,9770683 | 0,7057817 | 0,7465621 | 0,7863659 |
| germany_cpi | 0,5858029 | 0,6567352 | 1,0000000 | 0,6749995 | 0,7360533 | 0,5766805 | 0,6926212 |
| italy_cpi | 0,8816498 | 0,9770683 | 0,6749995 | 1,0000000 | 0,7540024 | 0,7600933 | 0,7644961 |
| japan_cpi | 0,7205414 | 0,7057817 | 0,7360533 | 0,7540024 | 1,0000000 | 0,8570803 | 0,7634052 |
| uk_cpi | 0,8544959 | 0,7465621 | 0,5766805 | 0,7600933 | 0,8570803 | 1,0000000 | 0,8940935 |
| usa_cpi | 0,8730004 | 0,7863659 | 0,6926212 | 0,7644961 | 0,7634052 | 0,8940935 | 1,0000000 |
Os países selecionados possuem economias já desenvolvidas e bastante conectadas entre si, por isso há este comportamento parecido nas taxas de inflação. A correlação é alta não apenas entre os EUA e os outros países, por conta desta conexão entre as economias.
c. Se você constatar que as taxas de inflação dos seis países evoluem no mesmo sentido que a dos Estados Unidos, isso sugere que a inflação dos Estados Unidos “causa” inflação nos outros países? Justifique.
Com estes dados não é possível verificar se há uma correlação espúria entre as variáveis, portanto não consigo afirmar se a variação na inflação dos EUA causa variação na inflação dos outros países. Mas pelo que lembro das aulas de macroeconomia, se um país está tendo inflação, sua moeda tende a se desvalorizar frente à outras moedas e se um país importa de outro que está tendo uma desvalorização cambial, ocorrerá uma queda no custo de importação e consequentemente uma pressão para redução de preços.
1.3 A Tabela 1.4 apresenta as taxas de câmbio em sete países industrializados, no período 1985 - 2006. Exceto no caso do Reino Unido, as taxas de câmbio estão definidas como unidades de moeda estrangeira por um dólar; no caso do Reino Unido, a taxa de câmbio é dada como o número de dólares por uma libra esterlina.
a. Represente graficamente a evolução das taxas de câmbio ao longo do tempo e comente sobre o comportamento geral dessa evolução.
# Trazendo o dataset para o exercício
table_1.4_exchange_rate <-
readr::read_delim(file = paste(dataset_path,
"table_1.4_exchange_rate.txt",
sep = ""),
delim = "\t")
table_1.4_exchange_rate %>%
mutate(Ano = as.character(Ano)) %>%
head(5) %>%
knitr::kable(format.args = list(big.mark = ".", decimal.mark = ","))| Ano | Australia | Canada | China | Japao | Mexico | Coreia.sul | Suecia | Suica | Reino.unido |
|---|---|---|---|---|---|---|---|---|---|
| 1985 | 0,7003 | 1,3659 | 2,9434 | 238.4700 | 0,257 | 872,45 | 8,6032 | 2,4552 | 1,2974 |
| 1986 | 0,6709 | 1,3896 | 3,4616 | 168.3500 | 0,612 | 884,60 | 7,1273 | 1,7979 | 1,4677 |
| 1987 | 0,7014 | 1,3259 | 3,7314 | 144.6000 | 1,378 | 826,16 | 6,3469 | 1,4918 | 1,6398 |
| 1988 | 0,7841 | 1,2306 | 3,7314 | 128.1700 | 2,273 | 734,52 | 6,1370 | 1,4643 | 1,7813 |
| 1989 | 0,7919 | 1,1842 | 3,7673 | 138.0700 | 2,461 | 674,13 | 6,4559 | 1,6369 | 1,6382 |
Antes de plotar o gráfico, vou fazer um ajuste para o Reino Unido para representar a mesma unidade de medida que os outros países (unidades de moeda local para adquirir 1 dólar).
table_1.4_exchange_rate %>%
mutate(Reino.unido = 1/Reino.unido) %>% # Ajustando o Reino Unido
tidyr::gather("country", "values", 2:10) %>%
mutate(values = as.numeric(values)) %>%
ggplot2::ggplot()+
geom_col(mapping = aes(x = Ano, y = values, fill = country), alpha = .6)+
scale_y_continuous(labels = scales::comma)+
scale_fill_brewer(type = "qual", palette = 3)+
theme_graph()+
theme(legend.position = "none",
axis.text.x = element_text(angle = 90))+
facet_wrap(~country, scales = "free_y")+
labs(title = "Taxa de Câmbio de Países Selecionados",
subtitle = "Unidade de moeda local por 1 dólar",
y = "Taxa de Câmbio",
x = "")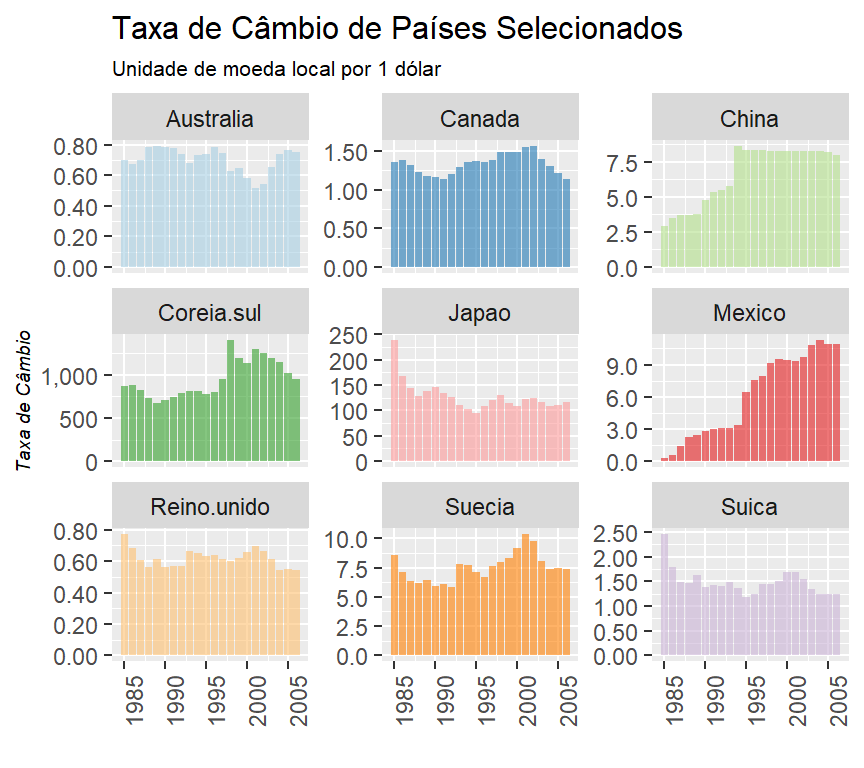
De maneira geral, apenas o México mostrou uma tendência de desvalorização de sua taxa de câmbio. Os outros países parecem ter a taxa de câmbio sob controle.
b. Diz-se que o dólar apreciou-se quando pode comprar mais unidades de moeda estrangeira. Opostamente, diz-se que se depreciou quando compra menos unidades da moeda estrangeira. No período 1985–2006, qual foi o comportamento geral do dólar dos Estados Unidos? Aproveite para pesquisar em algum livro de macroeconomia ou de economia internacional os fatores que determinam a apreciação ou depreciação de uma moeda.
O comportamento foi variado entre os países selecionados. Em alguns (Suíça, Japão e Reino Unido) houve desvalorização do dólar e em outros (México, China e Coréia do Sul), houve valorização.
1.4 A Tabela 1.5 apresenta os dados relativos à oferta monetária, no conceito de M1, que aparecem na Figura 1.5. Você poderia apresentar razões para o aumento da oferta de moeda no período considerado?
table_1.5_currency_m1_volume <-
readr::read_delim(file = paste(dataset_path,
"table_1.5_currency_m1_volume.txt",
sep = ""),
delim = "\t")
# Amostra do dataset
table_1.5_currency_m1_volume %>%
head(5) %>%
knitr::kable(format.args = list(big.mark = ".", decimal.mark = ","))| period | month_1 | month_2 | month_3 | month_4 | month_5 | month_6 |
|---|---|---|---|---|---|---|
| 1959:01 | 138,9 | 139,4 | 139,7 | 139,7 | 140,7 | 141,2 |
| 1959:07 | 141,7 | 141,9 | 141,0 | 140,5 | 140,4 | 140,0 |
| 1960:01 | 140,0 | 139,9 | 139,8 | 139,6 | 139,6 | 139,6 |
| 1960:07 | 140,2 | 141,3 | 141,2 | 140,9 | 140,9 | 140,7 |
| 1961:01 | 141,1 | 141,6 | 141,9 | 142,1 | 142,7 | 142,9 |
Esta tabela precisa ser tratada para poder ser analisada de maneira fácil. Veja que há 6 colunas para 6 meses de dados e os anos contemplam duas linhas. Será necessário ajustar para que cada mês fique em uma linha e o dataset tenha os campos ‘ano’, ‘mês’ e ‘valor (m1)’.
table_1.5_currency_m1_volume %>%
tidyr::gather("month", "value", 2:7) %>%
filter(!is.na(value)) %>%
mutate(semester = as.numeric(stringr::str_sub(string = period, start = 6, end = 7)),
year = stringr::str_sub(string = period, start = 0, end = 4),
month = as.numeric(stringr::str_sub(string = month, start = 7, end = 7))-1+semester) %>%
select(year, month, value) %>%
mutate(year_and_month = paste(year, month, sep = "/")) -> table_1.5_adj
table_1.5_adj %>%
head(5) %>%
knitr::kable(format.args = list(big.mark = ".", decimal.mark = ","))| year | month | value | year_and_month |
|---|---|---|---|
| 1959 | 1 | 138,9 | 1959/1 |
| 1959 | 7 | 141,7 | 1959/7 |
| 1960 | 1 | 140,0 | 1960/1 |
| 1960 | 7 | 140,2 | 1960/7 |
| 1961 | 1 | 141,1 | 1961/1 |
Agora podemos plotar o gráfico conforme solicitado e tentar analisar o aumento no período considerado.
table_1.5_adj %>%
ggplot2::ggplot()+
geom_line(mapping = aes(x = year_and_month, y = value, group = 1))+
scale_y_continuous(labels = scales::comma)+
scale_x_discrete(breaks = c("1960/5","1970/5","1980/5","1990/5","1999/1"))+
theme_graph()+
labs(title = "Oferta Monetária",
subtitle = "M1: Moeda em poder do público + Reservas Bancárias",
x = "",
y = "M1")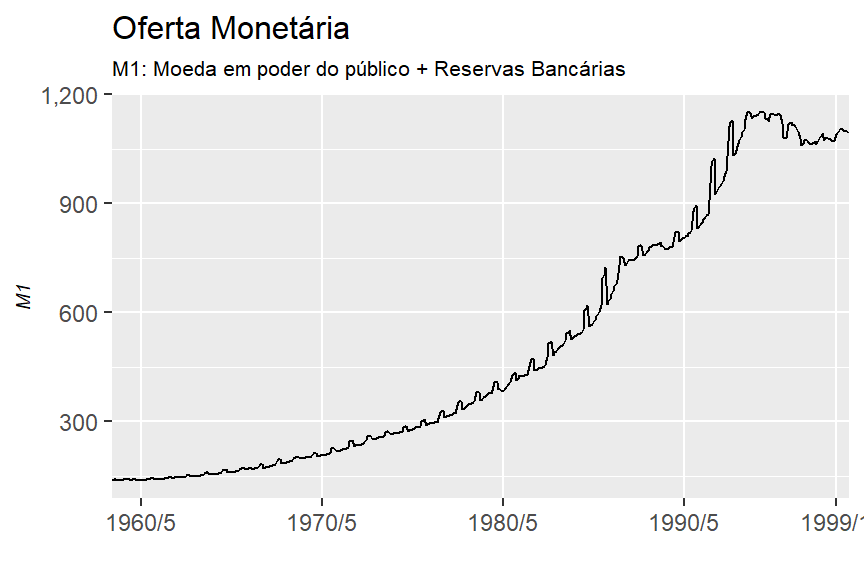
O crescimento pode ser atribuído ao aumento de oferta de crédito pelo governo e também ao crescimento econômico, que faz as pessoas sacarem seus investimentos para consumo ou investimento.
1.7 Os dados apresentados na Tabela 1.6 foram divulgados na edição do The Wall Street Journal de 1º de março de 1984. Relacionam o orçamento de publicidade (em milhões de dólares) de 21 empresas em 1983 com as impressões retidas, semanalmente, pelos que viram os produtos anunciados por essas empresas. Os dados foram obtidos em uma pesquisa realizada com 4 mil adultos, em que foi pedido aos usuários dos produtos que citassem um comercial da categoria do produto que tivessem assistido na semana anterior.
Vamos importar o dataset do Github e ver uma amostra dos valores.
# Este arquivo está separado por ';' ao invés de '\tab'
table_1.6_advertising <-
readr::read_delim(file = paste(dataset_path,
"table_1.6_advertising.txt",
sep = ""),
delim = "\t") %>%
mutate(impressions = as.numeric(impressions),
investment = as.numeric(investment))
# Amostra do dataset
table_1.6_advertising %>%
head(5) %>%
knitr::kable(format.args = list(big.mark = ".", decimal.mark = ","))| impressions | investment | company |
|---|---|---|
| 32,1 | 50,1 | Miller_Lite |
| 99,6 | 74,1 | Pepsi |
| 11,7 | 19,3 | Stroh |
| 21,9 | 22,9 | Fed_Express |
| 60,8 | 82,4 | Burger_King |
a. Trace um gráfico com as impressões no eixo vertical e os gastos com publicidade no eixo horizontal.
table_1.6_advertising %>%
ggplot2::ggplot()+
geom_point(mapping = aes(x = investment, y = impressions),
shape = 2,
color = "steel blue")+
theme_graph()+
labs(title = "Impressões vs Investimento em Publicidade",
subtitle = "Impressões Retidas nos Proutos Anunciados",
x = "Investimento em Publicidade (milhões de US$)",
y = "Impressões Retidas em Produtos Anunciados")
b. O que você poderia dizer sobre a natureza da relação entre as duas variáveis?
Apesar de existir uma correlação (notada pelo gráfico, não estatísticamente comprovada), ela pode não ser linear.
c. Examinando o gráfico, você acha que vale a pena anunciar? Pense em todos os comerciais veiculados em finais de campeonatos de esportes ou no horário nobre.
Parece valer a pena anunciar, porém não uma quantia acima de 100 milhões de dólares.
Capítulo 2
2.14. Com os dados da Tabela 2.7 relativos aos Estados Unidos nos período 1980-2006:
a. Represente graficamente a relação entre a taxa de participação dos homens na força de trabalho civil e a taxa de desemprego civil dos homens. Trace, a olho, uma linha de regressão que passe pelos pontos. A priori, qual a relação esperada entre as duas variáveis e em que teoria econômica está embasada? O diagrama de dispersão respalda essa teoria?
table_2.7_labour_market <-
readr::read_delim(file = paste(dataset_path,
"table_2.7_labour_market.txt",
sep = ""),
delim = " ")
# Amostra do dataset
table_2.7_labour_market %>%
head(5) %>%
knitr::kable(format.args = list(big.mark = ".", decimal.mark = ","))| year | share_men_work_force | share_women_work_force | unemployment_men | unemployment_women | avg_hourly_earning_men | avg_hourly_earning_women |
|---|---|---|---|---|---|---|
| 1.980 | 77,4 | 51,5 | 6,9 | 7,4 | 7,99 | 6,84 |
| 1.981 | 77,0 | 52,1 | 7,4 | 7,9 | 7,88 | 7,43 |
| 1.982 | 76,6 | 52,6 | 9,9 | 9,4 | 7,86 | 7,86 |
| 1.983 | 76,4 | 52,9 | 9,9 | 9,2 | 7,95 | 8,19 |
| 1.984 | 76,4 | 53,6 | 7,4 | 7,6 | 7,95 | 8,48 |
O dataset está em um formato não muito organizado (‘tidy’), pois está com as variáveis duplicadas para representar homens e mulheres. Vou ajustar o dataset para agrupar as variáveis e separar as linhas em ‘men’/‘women’.
table_2.7_labour_market %>%
select(year,
share_men_work_force,
share_women_work_force) %>%
tidyr::gather("gender","values",2:3) %>%
inner_join(table_2.7_labour_market %>%
select(year,
unemployment_men,
unemployment_women) %>%
tidyr::gather("gender","values",2:3),
by = c("year" = "year")) %>%
inner_join(table_2.7_labour_market %>%
select(year,
avg_hourly_earning_men,
avg_hourly_earning_women) %>%
tidyr::gather("gender","values",2:3),
by = c("year" = "year")) %>%
mutate(gender.x = ifelse(gender.x == "share_men_work_force","men","women")) %>%
mutate(gender = gender.x,
share_work_force = values.x,
unemployment_rate = values.y,
hourly_wage = values) %>%
select(year,
gender,
share_work_force,
unemployment_rate,
hourly_wage) -> table_2.7_labour_market_adjVeja a tabela ajustada. Talvez desse para fazer o ajuste com menos código, mas no fim o resultado deu certo.
table_2.7_labour_market_adj %>%
head(5) %>%
knitr::kable()| year | gender | share_work_force | unemployment_rate | hourly_wage |
|---|---|---|---|---|
| 1980 | men | 77.4 | 6.9 | 7.99 |
| 1980 | men | 77.4 | 6.9 | 6.84 |
| 1980 | men | 77.4 | 7.4 | 7.99 |
| 1980 | men | 77.4 | 7.4 | 6.84 |
| 1981 | men | 77.0 | 7.4 | 7.88 |
table_2.7_labour_market_adj %>%
filter(gender == "men") %>%
ggplot2::ggplot()+
geom_point(mapping = aes(x = share_work_force, y = unemployment_rate))+
theme_graph()+
labs(title = "Relação entre Participação na Força \nde Trabalho e Taxa de Desemprego",
subtitle = "Grupo de Homem apenas",
x = "Participação (%) no mercado de trabalho",
y = "Taxa (%) de Desemprego")
b. Faça o mesmo para as mulheres
table_2.7_labour_market_adj %>%
filter(gender == "women") %>%
ggplot2::ggplot()+
geom_point(mapping = aes(x = share_work_force,
y = unemployment_rate))+
theme_graph()+
labs(title = "Relação entre Participação na Força \nde Trabalho e Taxa de Desemprego",
subtitle = "Grupo de Homem apenas",
x = "Participação (%) no mercado de trabalho",
y = "Taxa (%) de Desemprego")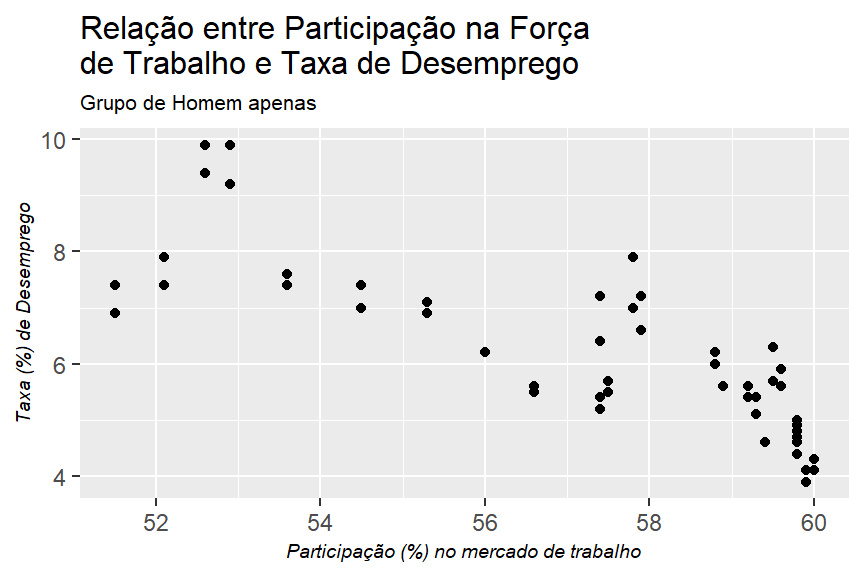
c. Agora, represente graficamente a taxa de participação de homens e mulheres em relação aos ganhos médios por hora (em dólares de 1982). (Você pode usar gráficos separados.) O que constatou? Como você justificaria isso?
table_2.7_labour_market_adj %>%
ggplot2::ggplot()+
geom_point(mapping = aes(x = share_work_force,
y = hourly_wage,
color = gender))+
theme_graph()+
scale_color_viridis_d()+
facet_grid(~gender, scales = "free")+
labs(title = "Relação Entre Salário e Participação \nno Mercado de Trabalho",
x = "Participação no Mercado de Trabalho (%)",
y = "Salário por Hora")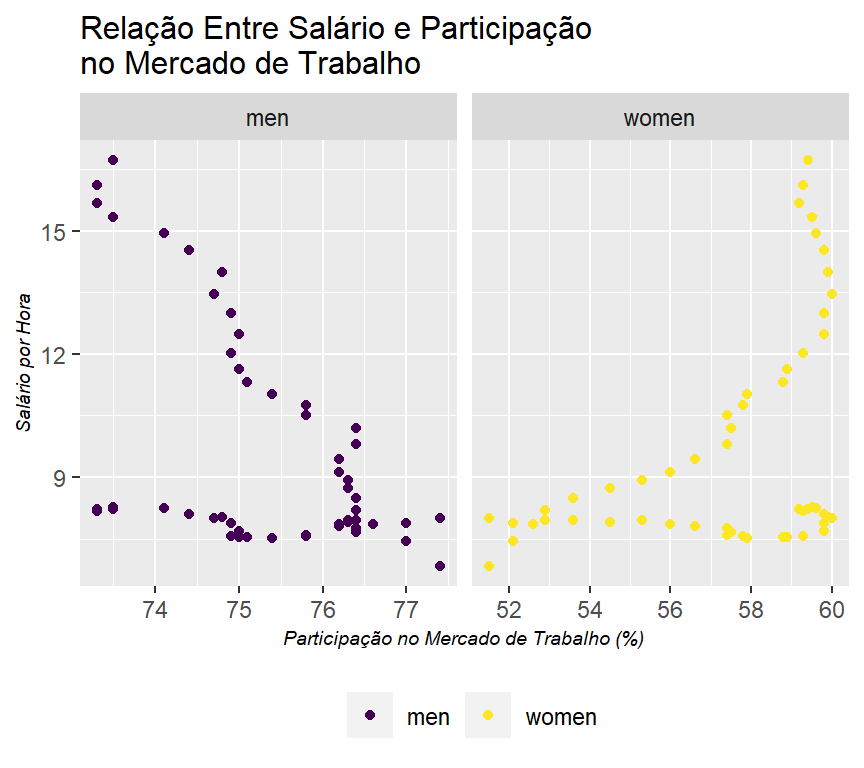
2.15. A Tabela 2.8 apresenta dados sobre despesas com alimentação e gastos totais, em rupias, para uma amostra de 55 domicílios rurais da Índia. (No início de 2000, um dólar americano era equivalente a cerca de 40 rupias indianas.)
table_2.8_expenses_in_india <-
readr::read_delim(file = paste(dataset_path,
"table_2.8_expenses_in_india.txt",
sep = ""),
delim = " ")
table_2.8_expenses_in_india %>%
head(5) %>%
kableExtra::kable()| food | total |
|---|---|
| 217 | 382 |
| 196 | 388 |
| 303 | 391 |
| 270 | 415 |
| 325 | 456 |
a. Represente graficamente os dados colocando no eixo vertical as despesas com alimentação e no eixo horizontal os gastos totais. Trace uma linha de regressão.
table_2.8_expenses_in_india %>%
ggplot2::ggplot()+
geom_point(mapping = aes(x = total, y = food),
shape = 2,
color = "dark orange")+
theme_graph()+
labs(title = "Despesas Totais vs Despesas com Alimentação",
x = "Despesas Totais",
y = "Despesas com Alimentação")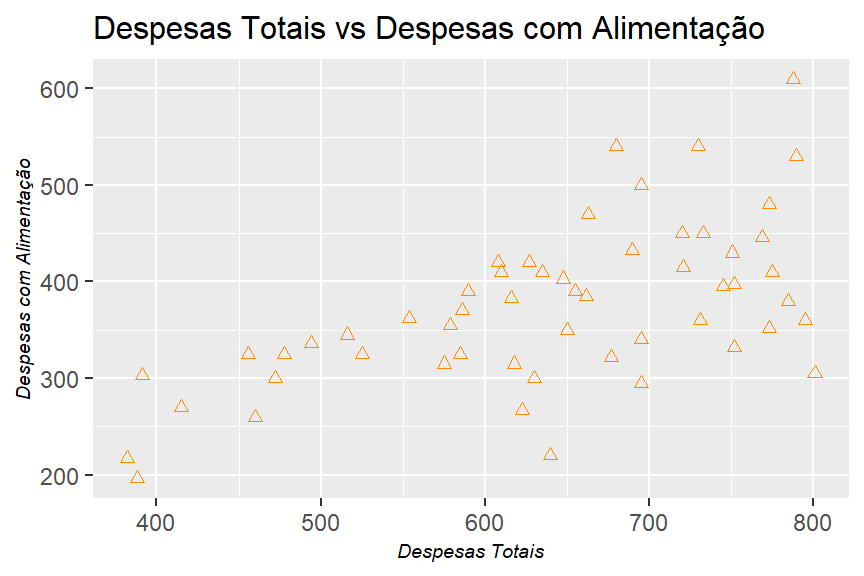
b. Que conclusões gerais você pode tirar deste exemplo?
A correlação é mais para famílias de baixa renda (com despesas totais abaixo de 600 rupias), visto que a maior parte dos gastos se concentra em itens básicos de alimentação. Porém, no geral, pode-se concluir com base neste teste visual, que há uma correlação entre as duas variáveis.
c. Você esperaria, a priori, que as despesas com alimentação aumentassem linearmente com o aumento das despesas totais, independentemente do nível destas? Por quê? Utilize a despesa total como uma proxy para o nível de renda total.
Não esperaria, visto que com o aumento do nível de renda a necessidade de se comprar mais alimentos não aumentará na mesma magnitude.
2.16. A Tabela 2.9 apresenta dados sobre a pontuação média do Teste de Aptidão Escolar (SAT) para os estudantes que se preparavam para ingressar no ensino superior no período 1967-1990.
table_2.9_sat_scores <-
readr::read_delim(file = paste(dataset_path,
"table_2.9_sat_scores.txt",
sep = ""),
delim = " ")
table_2.9_sat_scores %>%
head(5) %>%
kableExtra::kable()| year | men_verbal_score | wonem_verbal_score | verbal_score_total | men_math_score | women_math_score | math_score_total |
|---|---|---|---|---|---|---|
| 1972 | 531 | 529 | 530 | 527 | 489 | 509 |
| 1973 | 523 | 521 | 523 | 525 | 489 | 506 |
| 1974 | 524 | 520 | 521 | 524 | 488 | 505 |
| 1975 | 515 | 509 | 512 | 518 | 479 | 498 |
| 1976 | 511 | 508 | 509 | 520 | 475 | 497 |
a. Use o eixo horizontal para os anos e o eixo vertical para a pontuação obtida para traçar as notas nas provas de aptidão verbal e matemática obtidas por homens e mulheres, separadamente.
verbal_graph <-
table_2.9_sat_scores %>%
ggplot2::ggplot(mapping = aes(x = year))+
geom_line(mapping = aes(y = men_verbal_score, color = "men|verbal"))+
geom_line(mapping = aes(y = wonem_verbal_score, color = "women|verbal"))+
scale_color_manual(values = c("men|verbal" = "blue",
"women|verbal" = "red"),
name = "")+
theme_graph()+
labs(x = "",
y = "")
math_graph <-
table_2.9_sat_scores %>%
ggplot2::ggplot(mapping = aes(x = year))+
geom_line(mapping = aes(y = men_math_score, color = "men|math"))+
geom_line(mapping = aes(y = women_math_score, color = "women|math"))+
scale_color_manual(values = c("men|math" = "blue",
"women|math" = "red"),
name = "")+
theme_graph()+
labs(x = "",
y = "")
verbal_graph + math_graph +
patchwork::plot_annotation(title = "Comparativo de Notas Entre os Gêneros",
subtitle = "Teste SAT dos EUA")
b. Que conclusões gerais você tirou desses gráficos?
- Homens se saem melhores em ambos os testes e (ii) o teste de matemática ou foi ficando mais fácil ao longo dos anos ou os alunos foram se preparando melhor para fazê-lo. Também nota-se uma correlação entre os desempenhos em ‘Verbal’ e ‘Math’.
c. Conhecendo a pontuação de homens e mulheres nos testes de aptidão verbal, você poderia prever suas notas em matemática?
Analisando a série temporal do exercício ‘a’, parece ser possível esta regressão.
d. Represente graficamente as notas de matemática das mulheres em relação às dos homens. O que você observa?
table_2.9_sat_scores %>%
ggplot2::ggplot()+
geom_point(mapping = aes(x = women_math_score, y = men_math_score),
shape = 2,
color = "dark orange")+
theme_graph()+
labs(title = "Relação Entre Nota de Mulheres e Homens",
subtitle = "Exame de Matemática (SAT)",
x = "Mulheres",
y = "Homens")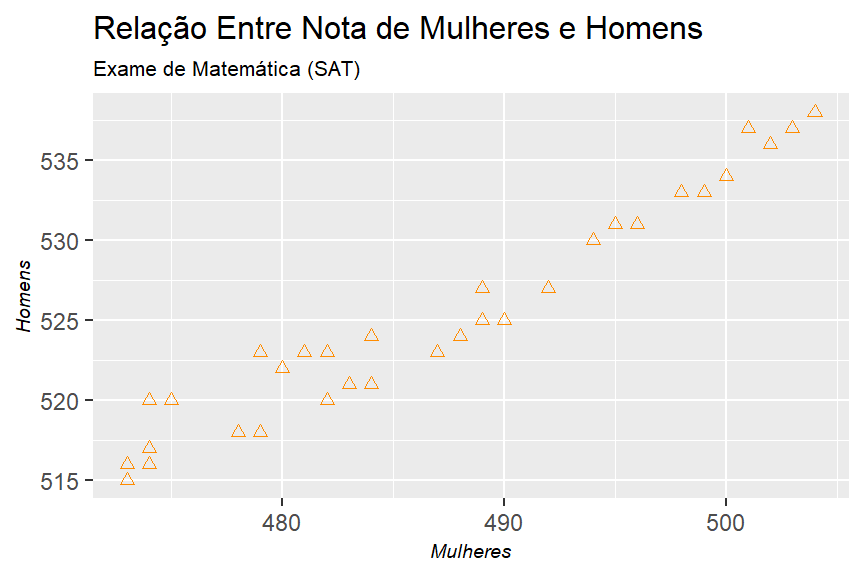
Capítulo 3
3.18. Na Tabela 3.5 está a classificação de dez estudantes nas provas parcial e final de estatística. Calcule o coeficiente de correlação de rankings de Spearman e interprete os resultados.
Como a tabela 3.5 é pequena, vou colocar os valores manualmente.
table_3.5 <-
data.frame(parcial_test = c(1,3,7,10,9,5,4,8,2,6),
final_test = c(3,2,8,7,9,6,5,10,1,4),
student = c("a","b","c","d","e","f","g","h","i","j"))cor.test(x = table_3.5$parcial_test,
y = table_3.5$final_test,
method = "spearman")##
## Spearman's rank correlation rho
##
## data: table_3.5$parcial_test and table_3.5$final_test
## S = 26, p-value = 0.004459
## alternative hypothesis: true rho is not equal to 0
## sample estimates:
## rho
## 0.84242423.19. A relação entre a taxa de câmbio nominal e os preços relativos. Com base nas observações anuais de 1985 a 2005, obteve-se a seguinte regressão, em que Y D taxa de câmbio do dólar canadense em relação ao dólar americano (DC/$) e X D razão do IPC americano pelo IPC canadense, isto é, X representa os preços relativos dos dois países:
a. Interprete a regressão. Como você interpretaria r²?
R: r² em 44% indica que a variação de Y possui outras variáveis explicativas que precisam ser inseridas no modelo. O erro padrão está baixo (acredito que seja estatisticamente significativo no modelo), portanto apesar de um r² baixo, o modelo se mostra confiável na explicação das variações de Y.
b. O valor positivo de X_t faz sentido econômico? Qual a teoria econômica em que se embasa?
R: Faz sentido, visto que \(X_t\) indica a razão entre Inflação dos EUA e do Canadá, e sabendo que a inflação corri o poder de compra da moeda e impacta na taxa de câmbio, se a Inflação dos EUA estiver maior que a do Canadá, a relação (DC/$) será afetada, onde o dólar ficará mais fraco frente ao dólar canadense (gerando aumento em Y, explicado pelo valor positivo de \(X_t\)).
c. Suponha que X seja redefinido como a razão entre o IPC canadense e o IPC americano. Isso mudaria o sinal de X? Por quê?
R: Mudaria, visto que Y continuaria sendo (DC/$).
3.20. A Tabela 3.6 apresenta dados relativos a índices de produção por hora (X) e remuneração real por hora (Y) para os setores empresarial e empresarial não agrícola da economia dos Estados Unidos no período 1960-2005. O ano-base dos índices é 1992 D 100 e os índices foram ajustados sazonalmente
table_3.6_wage_and_productivity <-
readr::read_delim(file = paste(dataset_path,
"table_3.6_wage_and_productivity.txt",
sep = ""),
delim = " ") %>%
tidyr::gather("metric","value",2:5) %>%
mutate(value = value/10) %>%
tidyr::spread("metric","value")table_3.6_wage_and_productivity %>%
head(5) %>%
knitr::kable(format.args = list(big.mark = ".",
decimal.mark = ","))| year | corporate | corporate_wages | non_agricultural | non_agricultural_wages |
|---|---|---|---|---|
| 1.960 | 48,9 | 60,8 | 51,9 | 63,3 |
| 1.961 | 50,6 | 62,5 | 53,5 | 64,8 |
| 1.962 | 52,9 | 64,6 | 55,9 | 66,7 |
| 1.963 | 55,0 | 66,1 | 57,8 | 68,1 |
| 1.964 | 56,8 | 67,7 | 59,6 | 69,3 |
a. Represente graficamente Y contra X para os dois setores da economia separadamente.
table_3.6_wage_and_productivity %>%
ggplot2::ggplot()+
geom_point(mapping = aes(x = corporate,
y = corporate_wages,
color = "Setor Empresarial"),
shape = 3)+
geom_point(mapping = aes(x = non_agricultural,
y = non_agricultural_wages,
color = "Setor Não Agrícola"),
shape = 2)+
scale_color_manual(values = c("Setor Empresarial" = "Steel Blue",
"Setor Não Agrícola" = "Dark Orange"),
name = "Setores")+
theme_graph()+
labs(title = "Relação Entre Produção por Hora e Salários",
x = "Produção por Hora",
y = "Salário")
b. Qual a teoria econômica que embasa a relação entre as duas variáveis? O gráfico de dispersão confirma a teoria?
R: Não sei dizer a teoria econômica que fundamenta esta relação direta, porém é esperado que a produtividade gere ganhos salariais, visto que se cria mais valor pra sociedade em um mesmo intervalo de tempo.
c. Estime uma regressão de MQO de Y contra X. Guarde os resultados para examiná-los novamente depois de estudar o Capítulo 5.
Cada setor terá uma regressão estimada.
- Setor Empresarial
table_3.6_wage_and_productivity %>%
lm(formula = "corporate_wages ~ corporate") %>%
summary() %>%
pander::pander()| Estimate | Std. Error | t value | Pr(>|t|) | |
|---|---|---|---|---|
| (Intercept) | 32.74 | 1.394 | 23.49 | 1.584e-26 |
| corporate | 0.6704 | 0.01567 | 42.78 | 1.724e-37 |
| Observations | Residual Std. Error | \(R^2\) | Adjusted \(R^2\) |
|---|---|---|---|
| 46 | 2.384 | 0.9765 | 0.976 |
table_3.6_wage_and_productivity %>%
lm(formula = "non_agricultural_wages ~ non_agricultural") %>%
summary() %>%
pander::pander()| Estimate | Std. Error | t value | Pr(>|t|) | |
|---|---|---|---|---|
| (Intercept) | 32.39 | 1.39 | 23.3 | 2.214e-26 |
| non_agricultural | 0.6711 | 0.0155 | 43.29 | 1.033e-37 |
| Observations | Residual Std. Error | \(R^2\) | Adjusted \(R^2\) |
|---|---|---|---|
| 46 | 2.244 | 0.9771 | 0.9765 |
3.23. A Tabela 3.8 apresenta dados do produto interno bruto (PIB) dos Estados Unidos no período 1959-2005.
table_3.8_usa_gdp_nominal_and_real <-
readr::read_delim(file = paste(dataset_path,
"table_3.8_usa_gdp_nominal_and_real.txt",
sep = ""),
delim = " ")table_3.8_usa_gdp_nominal_and_real %>%
head(5) %>%
knitr::kable(format.args = list(big.mark = ".",
decimal.mark = ","))| year | nominal_gdp | real_gdp |
|---|---|---|
| 1.959 | 506,6 | 2.441,3 |
| 1.960 | 526,4 | 2.501,8 |
| 1.961 | 544,7 | 2.560,0 |
| 1.962 | 585,6 | 2.715,2 |
| 1.963 | 617,7 | 2.834,0 |
a. Represente graficamente os dados do PIB em dólares correntes e em dólares constantes (de 2000) em relação ao tempo.
table_3.8_usa_gdp_nominal_and_real %>%
ggplot2::ggplot()+
geom_line(mapping = aes(x = year, y = nominal_gdp, color = "Nominal"))+
geom_line(mapping = aes(x = year, y = real_gdp, color = "Real"))+
scale_color_manual(values = c("Nominal" = "Dark Orange",
"Real" = "Steel Blue"))+
theme_graph()+
labs(title = "PIB dos EUA, Nominal e Real",
x = "Year",
y = "GDP")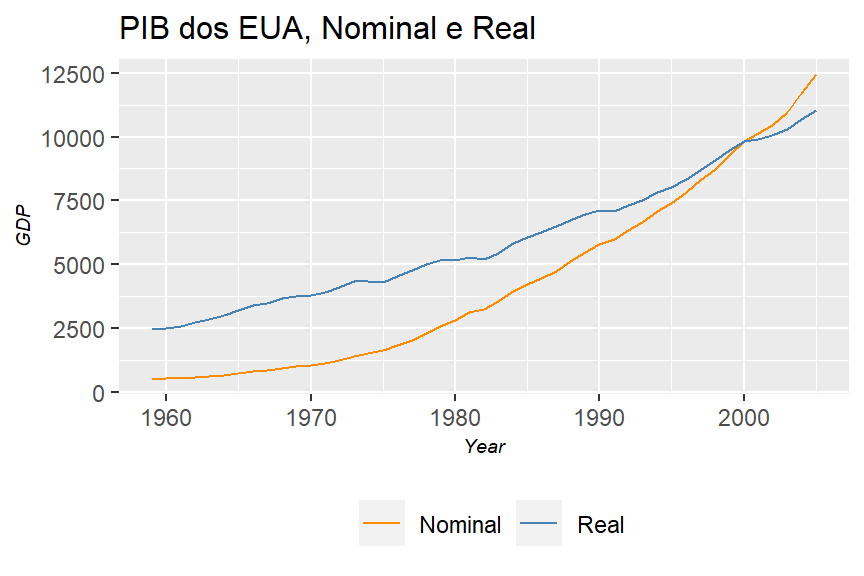
b. Denotando o PIB por Y e o tempo por X (medido em uma sequência cronológica em que l represente 1959, 2, 1960 e assim por diante até 47 para 2005), veja se o seguinte modelo ajusta-se aos dados do PIB:
\[y_t = \beta_1 + \beta_2 x_t + \mu_t\]
Apenas pelo gráfico dá para se notar uma relação entre tempo e variação do PIB. Algo que é bem comum em séries temporais, onde se incluem modelos de regressão para fazer o ‘forecasting’. Vamos ver se o modelo se adequa bem aos dados.
- PIB Nominal
table_3.8_usa_gdp_nominal_and_real %>%
lm(formula = "nominal_gdp ~ year") %>%
summary() %>%
pander::pander()| Estimate | Std. Error | t value | Pr(>|t|) | |
|---|---|---|---|---|
| (Intercept) | -496268 | 21089 | -23.53 | 6.286e-27 |
| year | 252.6 | 10.64 | 23.74 | 4.367e-27 |
| Observations | Residual Std. Error | \(R^2\) | Adjusted \(R^2\) |
|---|---|---|---|
| 47 | 989.5 | 0.926 | 0.9244 |
- PIB Real
table_3.8_usa_gdp_nominal_and_real %>%
lm(formula = "real_gdp ~ year") %>%
summary() %>%
pander::pander()| Estimate | Std. Error | t value | Pr(>|t|) | |
|---|---|---|---|---|
| (Intercept) | -351335 | 9070 | -38.74 | 3.332e-36 |
| year | 180.3 | 4.576 | 39.39 | 1.597e-36 |
| Observations | Residual Std. Error | \(R^2\) | Adjusted \(R^2\) |
|---|---|---|---|
| 47 | 425.6 | 0.9718 | 0.9712 |
c. Como você interpretaria \(\beta_2\)?
Para ambas as variáveis (Nominal e Real), o tempo se mostra estatisticamente significativo (com valor p bastante baixo) e também nos dois modelos a capacidade de explicar variações em Y é alta (demonstrado pelo r²).