Análise de Resíduos em Modelos de Regressão Linear

Exemplo 1: Elasticidade preço x oferta na produção de cana de açúcar.

Este exemplo foi passado na minha aula de econometria em 2017. Na época o exercício foi realizado com o software EViews, por sorte eu guardei os dados e agora posso refazer o problema com mais facilidade com o uso do R.

No exercício, há a variável independente (X) sendo o preço da cana de açúcar e a variável dependente (Y) sendo a área plantada de cana de açúcar (representando uma proxy para a oferta do produto). O objetivo deste modelo é tentar quantificar a elasticidade da oferta em função do preço, ou seja, quantificar quão sensível é a oferta da cana de açúcar quando ocorre uma variações em seu preço. Os dados deste exercício estão no meu repositório do Github, vamos trazê-los com o comando abaixo, salvando-os na variável df (a.k.a data.frame):

df <- read.csv(file = "https://raw.githubusercontent.com/FranciscoPiccolo/franciscopiccolo.github.io/master/datasets/2019-09-05-residual_analysis_on_linear_regression_models/dataset_1.csv", sep = ";", dec = ",")

dim(df)

## [1] 34  3

Com a função dim podemos ver a dimensão deste dataset, com 34 registros e 3 colunas.

The data set for this example has 34 rows, with planted area and suggarcane price fields. Vamos ver uma amostra dos dados.

df[sample(nrow(df),5), ] %>%
    as_tibble()

## # A tibble: 5 x 3
##   period  area price
##    <int> <int> <dbl>
## 1     28   152 0.405
## 2     13   125 0.194
## 3     29   197 0.353
## 4     14   232 0.270
## 5     23   230 0.360

O modelo de regressão linear para este cenário será desenvolvido de acordo com a fórmula abaixo:

\[ lnY_t = \beta_0+\beta_1 (lnX_t) + \mu_t \]

Onde:

\(Y_t\) = Área plantada após a transformação com log natural (e)

\(X_t\) = Preço da cana de açúcar também após a transformação com log natural

\(\beta_0\) = Intercepto

\(\beta_1\) = Inclinação

\(\mu_t\) = Resíduos

Os dados precisam ter a aplicação do log natural, pois esta transformação faz com que as variações entre os períodos possam ser interpretadas como variações percentuais, e isso é necessário por conta de que a elasticidade é quantificada em termos percentuais. Esta característica ocorre apenas na transformação com logarítmo natural, se a transformação fosse feita com outros logs, a interpretação não seria válida.

O gráfico abaixo irá mostrar o comportamento das variáveis do dataset, bem como a curva de regressão linear, antes de aplicar a transformação log natural.

df %>% 
  ggplot()+
  geom_point(mapping = aes(x = price, y = area), shape = 2)+
  geom_smooth(mapping = aes(x = price, y = area), 
              method = "lm", 
              formula = y ~ x, 
              se = F, 
              lty = 2,
              color = "dark orange")+
  theme_graph()+
  labs(title = "Gráfico de dispersão das variáveis",
       x = "Preço da Cana de Açúcar",
       y = "Área Plantada")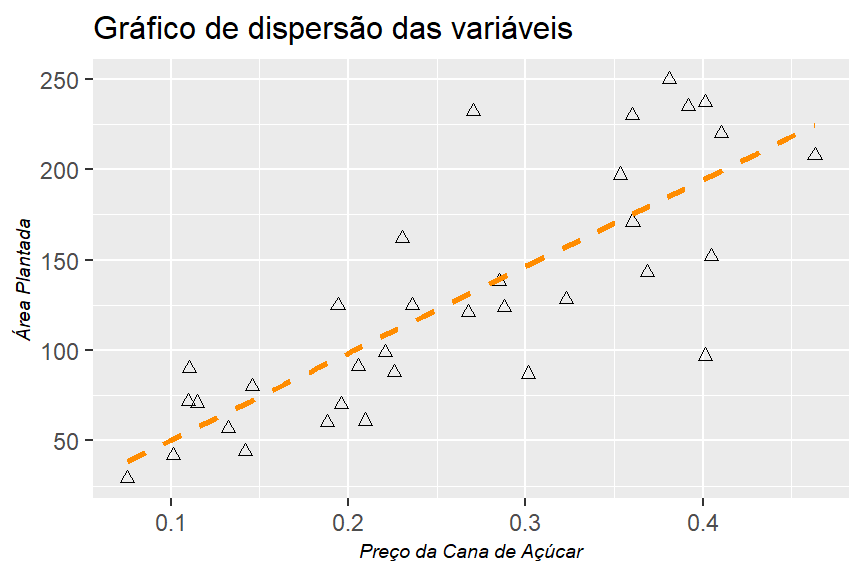

Podemos ver que há uma relação entre o preço do produto e sua oferta. Agora vamos aplicar o log natural no modelo de regressão. Para isso, o R nos fornece duas opções:

• Ajustar as variáveis no dataset e construir o modelo usando as variáveis ajustadas.

• Construir o modelo e indicar “dentro dele” que é necessário fazer a transformação antes de computar os resultados.

Vamos ver na prática como cada opção pode ser usada. O resultado final será idêntico.

Primeiro vou criar duas variáveis com os resultados dos dois métodos:

# Método 1, criando novos campos no dataset com a transformação log (e)
first_method <- 
  df %>% 
  mutate(area_log = log(area),
         price_log = log(price)) %>% 
  lm(formula = area_log ~ price_log)

second_method <- 
  df %>% 
  lm(formula = log(area) ~ log(price))

Com as duas variáveis criadas, vamos criar uma tabela comparando os principais resultados dos modelos:

data.frame("1º Método" = c(first_method$coefficients),
           "2º Método" = c(second_method$coefficients))

##             X1º.Método X2º.Método
## (Intercept)  6.1113284  6.1113284
## price_log    0.9705823  0.9705823

Conforme indicado, ambos os métodos geram o mesmo valor. Eu prefiro o segundo, que exige menos linhas de código. Com base nos coeficientes estimados, temos a seguinte equação:

\[\hat{Y} = 1.6416 + 0.9706X_1 + \mu\]

O resultado é estatisticamente significativo, visto que tanto o intercepto quanto a inclinação apresentam um valor-p baixo. Veja abaixo estes valores bem como o R².

second_method %>% summary()

## 
## Call:
## lm(formula = log(area) ~ log(price), data = .)
## 
## Residuals:
##      Min       1Q   Median       3Q      Max 
## -0.65076 -0.18823 -0.03096  0.24914  0.60492 
## 
## Coefficients:
##             Estimate Std. Error t value Pr(>|t|)    
## (Intercept)   6.1113     0.1686  36.254  < 2e-16 ***
## log(price)    0.9706     0.1106   8.773 5.03e-10 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 0.3088 on 32 degrees of freedom
## Multiple R-squared:  0.7063, Adjusted R-squared:  0.6972 
## F-statistic: 76.97 on 1 and 32 DF,  p-value: 5.031e-10

Apesar destes dados mostrarem que a reta se ajustou bem aos dados e que o modelo consegue explicar ~70% da variação na variável dependente, é preciso anda analisar os resíduos para poder ter confiança no resultado para fazer projeções. No gráfico abaixo, vamos ver como se distribui os resíduos do modelo.

model_residuals <- 
  data.frame(values = second_method$residuals)

Eu opto primeiro por analisar um histograma dos reísduos, pois ele indicará se a distribuição se assemelha a uma distribuição normal. Vamos ver isso no gráfico abaixo.

# Histogram
model_residuals %>% 
  ggplot()+
  geom_histogram(mapping = aes(x = values), fill = "steel blue")+
  theme_graph()+
  labs(title = "Distribuição dos Resíduos",
       x = "",
       y = "")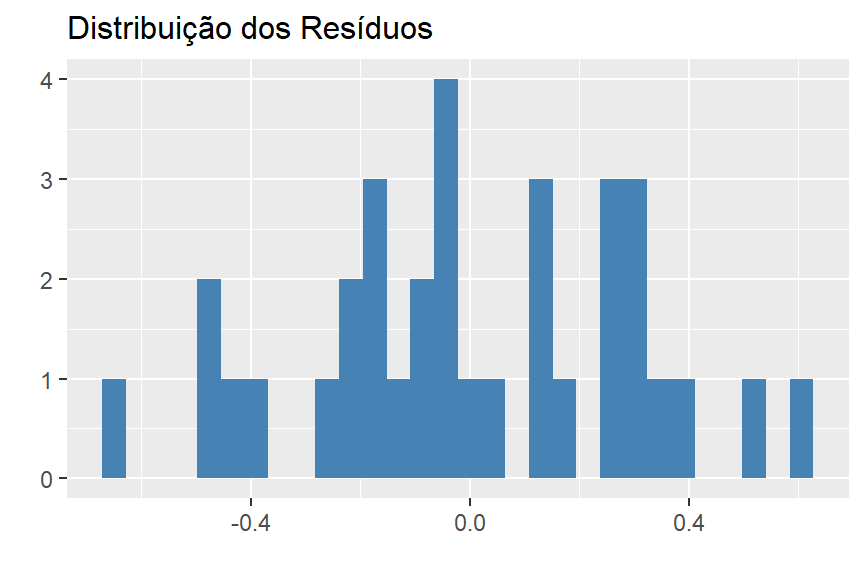

Aparentemente os resíduos se distribuem normalmente. Outro gráfico interessante para analisar é o q-q plot, que também indicará quão parecido com a distribuição normal é a distribuição de uma variável.

# q-q plot
model_residuals %>% 
  ggplot()+
  geom_qq(mapping = aes(sample = values))+
  labs(title = "Residuals' Q-Q plot",
       x = "",
       y = "")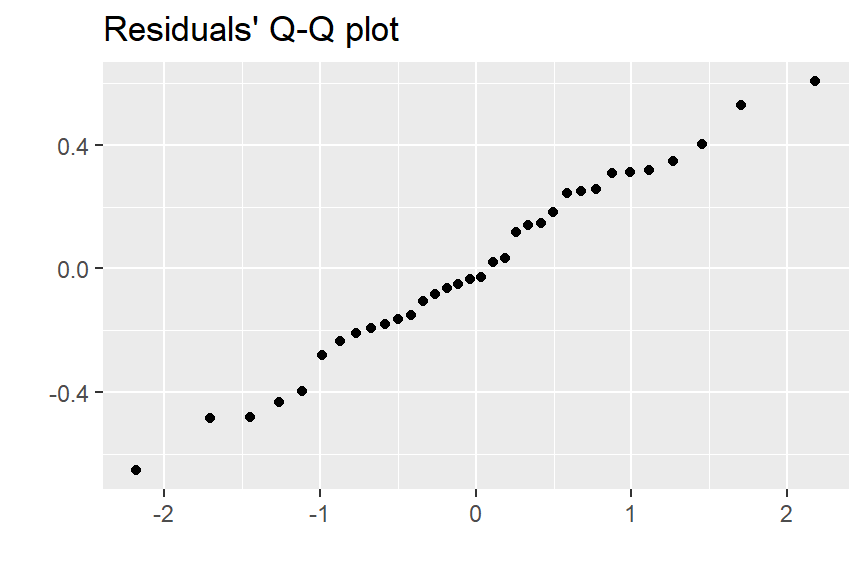

Este gráfico também aponta para a ideia de resíduos normalmente distribuídos. Apesar de estes métodos serem bons e práticos, as vezes é necessário usar métodos formais para gerar alguma conclusão. Para validação da independência no comportamento dos resíduos pode-se usar o teste Durbin Watson. O código abaixo realiza este teste.

# Necessário instalar e chamar o pacote 'lmtest'
lmtest::dwtest(df %>% 
                 lm(formula = log(area) ~ log(price)))

## 
##  Durbin-Watson test
## 
## data:  df %>% lm(formula = log(area) ~ log(price))
## DW = 1.2912, p-value = 0.009801
## alternative hypothesis: true autocorrelation is greater than 0

O resultado do teste foi de 1.2912, mas apenas com este valor não é possível fazer uma conclusão. Em conjunto com este valor, é preciso saber os valores limiares DL e DU, que podem ser encontrados nesta tabela. Para encontrar os valores com esta tabela, basta saber o número de observações no dataset (i.e. n = 33), o nível de significância do teste (i.e. 0.05) e os graus de liberdade (i.e. 1). Com isso, tem-se:

DL = 1.35

DU = 1.49

Tendo DW igual a 1.2912, acima de 0 e abaixo de DL, pode-se concluir que os resíduos são independentes.

Com isso, podemos concluir que de fato o modelo é confiável para realizar projeções, pois tanto os gráficos quanto o teste formal indicam que as premissas (iii) e (iv) estão sendo atendidas, como como as outras premissas. Desta forma, podemos concluir que há elasticidade na oferta de cana de açúcar com relação ao seu preço.